diffusionのコア部分をtoy datasetで実装
2022年はdiffusionを利用したtext-to-imageモデルによる画像生成が流行った。 2020年にDDPMの論文が出てから2年程度で実用的な意味でもSoTAな手法になったわけだが、transformerが出てきたときと同じような大きな流れである模様。
diffusionを改善・応用した手法は多く出てきており、それらをちゃんと理解するためにも基本的な部分を実装してみた。
diffusionが最初に出てきたと言われるのは2015年に出たこちらの論文のようだが
https://arxiv.org/abs/1503.03585
実応用として画像がGANのモデルと遜色のないレベルのクオリティで生成できることを初めて示したこちらの論文(DDPM)なのでこれを理解するのが良さそう。
https://arxiv.org/abs/2006.11239
どんなものか？
既にわかりやすい解説記事がたくさん上がっているので勉強には困らなかった。特にわかりやすかったものをまず貼っておく。
- https://data-analytics.fun/2022/02/03/understanding-diffusion-model/
- https://www.youtube.com/watch?v=DDGgKt_CyRQ&list=PLJOBpGoMd1MP3-wWMzBIDazmwk-aAPWjl
詳細はそちらに任せるが勉強のメモとして自分なりにわかったことを概要としてまとめておく。
背景として
- 複雑な特徴を学習するにはパラメータの多い大きなモデルが必要となるが、そのようなモデルは適切な学習やモデルの解析が難しい
- Flow型のような解析しやすいモデルもあるが、その分制約が強いため表現力も控えめになりがち
これらのメリット部分を併せ持つ形となっているのがdiffusion系のモデル。
1ステップを小さなガウシアンノイズの付与として多数回重ね合わせることで目的の分布（複雑な特徴を持つ画像など）を表現できる。1ステップ分の分布は当然目的の分布の学習に比べて容易である。また、その際にかかる数学的な制約はステップの幅を小さくすることだけでありFlow型のような表現力の制約がかからない （ただし、推論に時間がかかるというGANなどと比較した際のデメリットとして表れている）
diffusionのフローを最もよく表しているのが論文のこちらの図
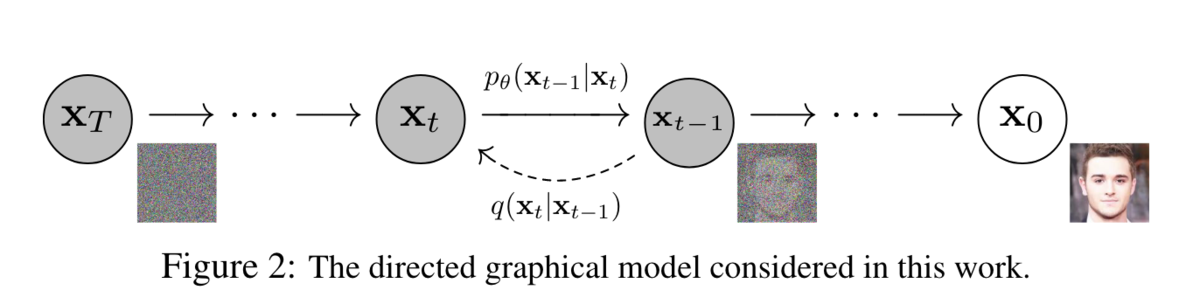
- 元データ(x0)にノイズを徐々に付与して完全なノイズ(xT)にするforward process
- 1step分のノイズ付与をqで表し、これはノイズとその付与割合を決めれば計算できる
- xTに適切なノイズを徐々に付与することでx0を復元するreverse process
- 1step分のノイズ付与をpで表し、これをデータに合わせて適切な分布になるよう学習したい
step数を十分に大きくして1step当たりのノイズが小さい場合、上記のp, qは同じ分布として表せることが過去の研究からわかっており、その状態に合致するstep数やノイズ付与割合とすることを前提に定式化する。
- VAEと同様に変分下界の最大化を目指す
- pの分散は固定値にして単純化
- pの平均μをニューラルネットワークで表現し、式変形によってノイズ推定問題に置き換え
- 実験によりそちらの方がパフォーマンスがよかったため
で、単純化された目的関数がこちら
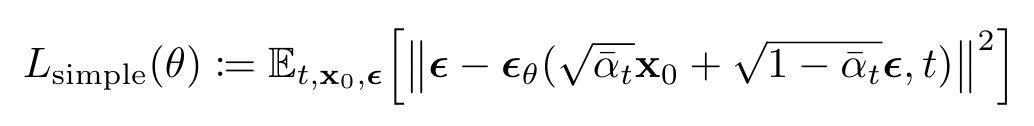時刻tにおけるノイズ付与されたデータから、そのときに付与された1step分のノイズを予測する形でとてもシンプル。
実装
実装の参考にしたのはこちら
https://huggingface.co/blog/annotated-diffusion
実装に必要な情報や各部分のコードがわかりやすく解説されている。
方針としては基本的に論文の内容に合わせるが、参考にするコードは上記のページなので完全には一致してないと思われる。また、diffusionのキモはステップごとのノイズ付与による学習と推論の部分なので、その部分に集中できるよう簡略化したtoy datasetを使うことにする。そうすると学習が短時間で済むし、NN部分は単純なMLPにしておけばよいので楽。
実装の全体はこちら
https://github.com/y-kamiya/diffusion/blob/a69af6f41658be7c4d6eabab92c310d38f1df7b9/src/toy.py
学習フローはこちらの通り
def q_sample(self, x0, t, e=None):
if e is None:
e = torch.randn_like(x0, device=self.config.device)
a_cum = self.a_cum[t].view(-1, 1)
return torch.sqrt(a_cum) * x0 + torch.sqrt(1 - a_cum) * e
def step(self, x):
e = torch.randn_like(x, device=self.config.device)
t = torch.randint(0, self.config.T, (x.shape[0],), device=self.config.device)
input = self.q_sample(x, t, e)
output = self.model(input, t)
loss = nn.functional.mse_loss(output, e)
データと同じ形状のガウシアンノイズとuniformにサンプルした時刻tに対し、その時点でのノイズ付与済みデータをforward processにより計算。それをinputとしてNNに時刻と共に渡し、出力と元のガウシアンノイズで二乗誤差を取ってlossとする。
推論フローはこちらの通り
@torch.no_grad()
def sample(self, n: int, xt=None, t_start=None):
...
ts = range(t_start, 0, -1)
for t in ts:
z = torch.randn((n, self.input_dim), device=self.config.device) if t > 1 else 0
e = self.beta[t] / torch.sqrt(1 - self.a_cum[t]) * self.model(xt, torch.tensor(t).repeat(n))
xt = (xt - e) / torch.sqrt(1 - self.beta[t]) + torch.sqrt(self.sigma[t]) * z
論文の図の通りにコード化しただけだが、私は最初はパラメータのルートを取り忘れるなどミスってたので注意。こういうのを間違えるととても時間がかかる（最終的に一つずつ突き合わせてようやく間違いに気づきました）
diffusionに関わるパラメータは論文の通りでbeta（ノイズ付与率）は線形に変化させて元データに近い時刻ほどノイズ付与が小さくなる設定。
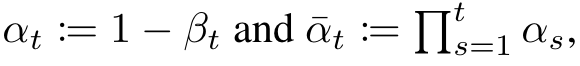
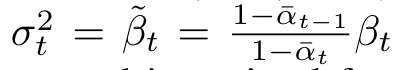
beta0 = 1e-4 betaT = 2e-2 self.beta = torch.linspace(beta0, betaT, config.T) self.a_cum = torch.cumprod(1 - self.beta, dim=0) a_cum_prev = torch.cat((torch.Tensor([0]), self.a_cum[:-1])) self.sigma = (1 - a_cum_prev) / (1 - self.a_cum) * self.beta
データセットは以下のどちらかの長さ4の数列
- 初項0~4、等差1
- 初項3~7、等差-1
[0,1,2,3], [1,2,3,4], ..., [4,5,6,7] [7,6,5,4], [6,5,4,3], ..., [3,2,1,0]
画像でいうところだと徐々に濃くなるor薄くなるグラデーションと同じ。画像の場合は8bit分(256階)だが今回はさらに小さく1bit分のみ。DDPMは画像に対して学習しているがそれの空間数、パターン数を極端に小さくしたものというイメージで。
class ToyDataset(utils.data.Dataset):
def __init__(self, dim=4, num_max=8):
self.dim = dim
self.num_max = num_max
data = []
for i in range(num_max - dim + 1):
data.append(list(range(i, i + dim)))
data.append(list(range(i + dim - 1, i - 1, -1)))
self.data = self.normalize(torch.Tensor(data)).repeat(1000, 1)
def __len__(self):
return len(self.data)
def __getitem__(self, index):
return self.data[index]
def normalize(self, x):
return 2 * x / (self.num_max - 1) - 1
def denormalize(self, x):
return (x + 1) * (self.num_max - 1) / 2
モデルに渡す際は各値を[-1, 1]の値にnormalize。これをやらないと学習がまったくうまくいかないので注意（特に最初に実装する際にはこういう部分は忘れやすい）
NNは単純な4層のMLP。隠れ層の次元は適当にデータの次元の100倍にしただけ。capacity不足でlossが小さくならないというのを防ぐためにちょっと大きめにしておいた。
class Model(nn.Module):
def __init__(self, dim, T):
super(Model, self).__init__()
self.dim = dim
self.T = T
self.fc1 = nn.Linear(dim + 1, 400)
self.fc2 = nn.Linear(400, 400)
self.fc3 = nn.Linear(400, 400)
self.fc4 = nn.Linear(400, dim)
def forward(self, x, t):
x = torch.cat((x, t.unsqueeze(-1) / self.T), dim=1)
x = F.relu(self.fc1(x.view(-1, self.dim + 1)))
x = F.relu(self.fc2(x))
x = F.relu(self.fc3(x))
return self.fc4(x)
時刻の印としては、最初の層だけ後ろに正規化した時刻をくっつけるだけにした。
結果
batch sizeの1024は適当、epochsはとても大きい値を設定してるだけで2分くらいのタイミングでCtrl-C。
$ python src/toy.py --batch_size 1024 --epochs 100000 --T 1000 [I 221231 14:04:04 toy:108] start training epoch 0 [I 221231 14:04:04 toy:132] [train] step: 0, loss: 1.257 [I 221231 14:04:04 toy:141] evaluate epoch 0 [I 221231 14:04:04 toy:108] start training epoch 1 [I 221231 14:04:04 toy:132] [train] step: 10, loss: 0.281 [I 221231 14:04:04 toy:108] start training epoch 2 [I 221231 14:04:04 toy:132] [train] step: 20, loss: 0.256 [I 221231 14:04:04 toy:108] start training epoch 3 ...
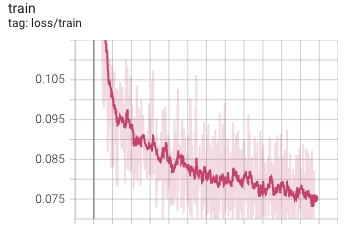
明らかにlossが下がり途中だがクオリティを上げることが目的じゃないので問題なし。
生成した結果（10個のベクトルを出力）
# 完全なノイズからの推論
$ python src/toy.py --T 1000 --sample_only
tensor([[1.9517, 3.0958, 3.9844, 5.0628],
[6.0427, 4.9173, 4.0149, 2.8960],
[4.1620, 5.0492, 6.0242, 7.0173],
[0.0311, 1.0536, 1.9632, 2.9813],
[3.9050, 2.9529, 1.9828, 1.0020],
[3.9972, 2.9883, 2.0320, 1.0342],
[6.1256, 5.0441, 4.0963, 2.9597],
[7.0356, 6.0315, 5.0716, 4.0767],
[6.0292, 4.9431, 3.9080, 2.9789],
[3.0652, 4.0415, 5.0707, 6.0714]])
# 初期状態指定で10ステップ分のみ推論
$ python src/toy.py --T 1000 --sample_only --name a --sample_from 1 2 3 4 --sample_t_start 10
tensor([[1.0400, 2.0241, 3.0691, 4.0281],
[0.9813, 2.0192, 3.0408, 4.0111],
[1.0063, 2.0051, 2.9564, 3.9855],
[1.0027, 2.0341, 2.9496, 4.0725],
[0.9470, 1.9784, 2.9939, 3.9557],
[1.0036, 1.9669, 3.0339, 3.9634],
[0.9800, 1.9579, 2.9750, 4.0107],
[1.0122, 1.9750, 2.9788, 3.9863],
[1.0134, 2.0207, 3.0561, 4.0768],
[1.0227, 1.9658, 2.9960, 3.9897]])
増えるパターンも減るパターンも表れており、初項もバラけているようにみえる。値自体もだいたいデータセットで定義した整数値に近いものになった。中間状態からの推論も指定した値に収束している。
デバッグという意味で時間がかかった部分をメモしておく
- 論文の式におけるパラメータの実装ミス
- データセットのnormalize, denormalizeがズレていた
- 結果として等差が0.7くらいの出力になったのだがおかしい部分に気づくまで時間がかかった
- 学習率が大きすぎた
- lossが小さくならない
まとめ
ひとまず実装してみて大枠として意図通り動いていそうな結果になった。U-NetやAttentionまわりの勉強も兼ねてその辺のも実装してみようか考え中。
実装しながら思ったこととして、一つのモデルをすべてのtに対して学習している点が面白い気がした。元の画像に対しノイズを付与して少しずつ変化させた画像を学習データとして使うので、augmentationやRNNの効果もアルゴリズムに組み込まれているのかもと思った。
理論的な話の部分でも、エネルギーベースモデルとの関連など知っていきたい部分があるのでdiffusionに関してはもう少し勉強したいと思う。
