2023-11-26

一枚の画像に映る人物に対するSMPL上での部分的なtexture mapを取り出す

denseposeとsmplの組み合わせはよく見かけるので勉強がてら一つやってみる。

実装も上がっており、やっていることも最小限に見えるのでこちらの論文の前処理を題材とする。

論文: https://arxiv.org/abs/1904.08645
実装: https://github.com/thmoa/tex2shape

やりたいことは、一枚の画像に映る人物をSMPLのtexture mapとして取り出すこと。

ちなみにSMPLについては以前記事を書いた
https://jsapachehtml.hatenablog.com/entry/2023/10/29/200455

人物領域の推定にはdenseposeを利用する

http://densepose.org/
image上の人物領域における各pixelについて以下を推定するモデル
- どのパーツに属するか
- そのパーツ上でどの位置にあるか
様々な姿勢の人物画像とそのSMPL mesh上での対応点のペアを学習データとしている

パーツ分けについては位置の回帰がしやすいよう独自の分け方をしており、SMPLの元のtexture mapとは異なるが、同じmeshを参照してるものなので相互に変換できる。

denseposeでのIUV map作成

こちらの画像をサンプルとして使う
https://github.com/thmoa/tex2shape/blob/303b94f/data/images/spotlight_001.jpg

denseposeは論文が出た時点と実装の管理方法が変わっていて、現在はdetectron2の一部として統合されていた。

元のrepo: https://github.com/facebookresearch/DensePose
今のrepo: https://github.com/facebookresearch/detectron2/tree/main/projects/DensePose

新しい方のrepoの実装を利用する。

論文にあるこちらの画像右のtexture map形式の画像を得ることが今回の目的であり、そのためにまず真ん中のようなIUV mapを得たい。

denseposeの推論にはこちらのスクリプトが用意されており、入力画像に対する推論結果が画像化できる
https://github.com/facebookresearch/detectron2/blob/main/projects/DensePose/doc/TOOL_APPLY_NET.md#visualization-mode

ただ、入力画像に推論結果のmaskを重ねて表示するもののようで、IUV map自体の画像を出力してくれるオプションはなかった。中を見てみると例えばこのようにIUVを利用してる部分がある。
https://github.com/facebookresearch/detectron2/blob/4e80df1/projects/DensePose/densepose/vis/densepose_results_textures.py#L51

なのでこれだけ出力するよう簡易なオプションを実装して使った。
https://github.com/y-kamiya/detectron2/commit/c44db8b3e146fa6ac89825645492f2278a1b8425

apply_net.pyのドキュメントを参考に以下のコマンドでIUV mapを出力

python apply_net.py show configs/densepose_rcnn_R_50_FPN_DL_s1x.yaml R_50_FPN_DL_s1x.pkl spotlight_001.jpg dp_iuv_map --output spotlight_001.png  -v

これで左ような画像(=spotlight_001.0001.png)が取得できる(右は入力画像)

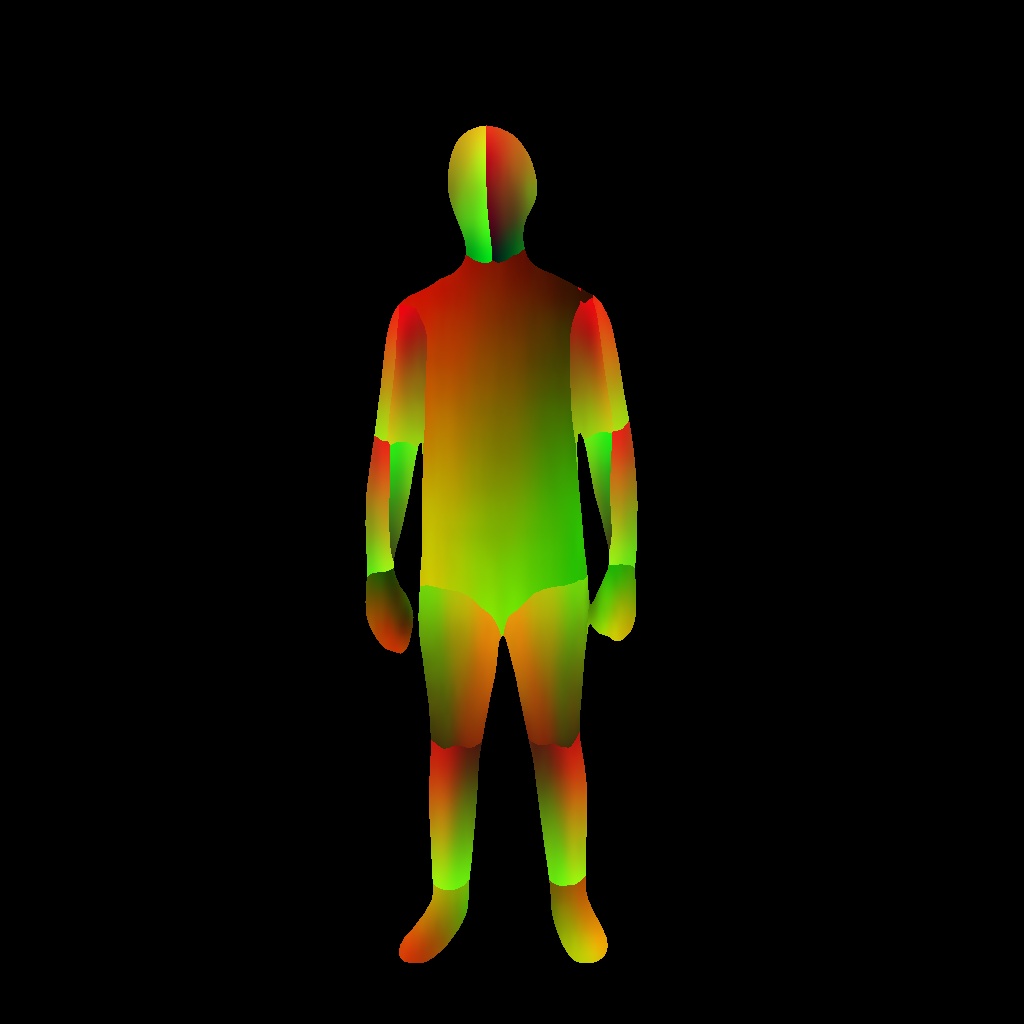
ちなみに環境構築に関してはこちらに書いてある通りで、python3.10系、torch==2.1.0でも問題なく動いた
https://github.com/facebookresearch/detectron2/blob/4e80df1/projects/DensePose/doc/GETTING_STARTED.md#installation-as-a-package

学習済みモデルについてはこちらから精度の高いものを選んで落とした
https://github.com/facebookresearch/detectron2/blob/4e80df1/projects/DensePose/doc/DENSEPOSE_IUV.md#-model-zoo-and-baselines

texture mapの作成

densepose用のformatからSMPLのformatへの変換部分について、論文著者が効率のためlookup tableを事前に用意したと書いてあり今回はそれを利用する

For easier mapping, we precompute a look-up table to convert from 24 DensePose UV maps to the single joint SMPL UV parameterization.

変換を行っているのはこちらの処理
https://github.com/thmoa/tex2shape/blob/504c69ee4a08f6e6ed42460645acd301f7fc680d/lib/maps.py#L6
入力画像の各pixel値をIUV mapが示すtexture map上の位置へコピーしている

この関数を使うように以下の簡易なスクリプト(=unwrap.py)を実装

import cv2
import os
import argparse
import numpy as np

from lib.maps import map_densepose_to_tex


def main(img_file, iuv_file):
    img = cv2.imread(img_file) / 255.
    iuv_img = cv2.imread(iuv_file)
    unwrap = (map_densepose_to_tex(img, iuv_img, 512) * 255).astype(np.int32)
    out_file = os.path.basename(img_file)
    cv2.imwrite(f"out/unwrap_{out_file}", unwrap)


if __name__ == '__main__':
    parser = argparse.ArgumentParser()
    parser.add_argument('image', type=str, help="Input image")
    parser.add_argument('iuv', type=str, help="Densepose IUV image")
    args = parser.parse_args()
    print(args)

    main(args.image, args.iuv)

実行

python unwrap.py spotlight_001.jpg spotlight_001.0001.png

出力

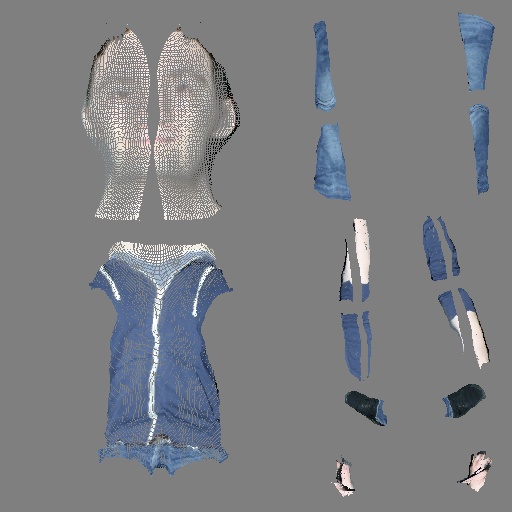
だいぶスカスカのtexture mapになるが、正面から見た一枚のみから抽出した部分的なものなのでこうなる。

ちなみに論文だと、これを入力としてpix2pixの形式でnormal mapとdisplacement mapを予測するよう学習し、入力画像の3d形状を推定している。

2023-11-26

一枚の画像に映る人物に対するSMPL上での部分的なtexture mapを取り出す

denseposeとsmplの組み合わせはよく見かけるので勉強がてら一つやってみる。

実装も上がっており、やっていることも最小限に見えるのでこちらの論文の前処理を題材とする。

論文: https://arxiv.org/abs/1904.08645
実装: https://github.com/thmoa/tex2shape

やりたいことは、一枚の画像に映る人物をSMPLのtexture mapとして取り出すこと。

ちなみにSMPLについては以前記事を書いた
https://jsapachehtml.hatenablog.com/entry/2023/10/29/200455

人物領域の推定にはdenseposeを利用する

http://densepose.org/
image上の人物領域における各pixelについて以下を推定するモデル
- どのパーツに属するか
- そのパーツ上でどの位置にあるか
様々な姿勢の人物画像とそのSMPL mesh上での対応点のペアを学習データとしている

denseposeでのIUV map作成

こちらの画像をサンプルとして使う
https://github.com/thmoa/tex2shape/blob/303b94f/data/images/spotlight_001.jpg

denseposeは論文が出た時点と実装の管理方法が変わっていて、現在はdetectron2の一部として統合されていた。

元のrepo: https://github.com/facebookresearch/DensePose
今のrepo: https://github.com/facebookresearch/detectron2/tree/main/projects/DensePose

新しい方のrepoの実装を利用する。

論文にあるこちらの画像右のtexture map形式の画像を得ることが今回の目的であり、そのためにまず真ん中のようなIUV mapを得たい。

なのでこれだけ出力するよう簡易なオプションを実装して使った。
https://github.com/y-kamiya/detectron2/commit/c44db8b3e146fa6ac89825645492f2278a1b8425

apply_net.pyのドキュメントを参考に以下のコマンドでIUV mapを出力

python apply_net.py show configs/densepose_rcnn_R_50_FPN_DL_s1x.yaml R_50_FPN_DL_s1x.pkl spotlight_001.jpg dp_iuv_map --output spotlight_001.png  -v

これで以下のような画像(=spotlight_001.0001.png)が取得できる

texture mapの作成

densepose用のformatからSMPLのformatへの変換部分について、論文著者が効率のためlookup tableを事前に用意したと書いてあり今回はそれを利用する

For easier mapping, we precompute a look-up table to convert from 24 DensePose UV maps to the single joint SMPL UV parameterization.

この関数を使うように以下の簡易なスクリプトを実装

import cv2
import os
import argparse
import numpy as np

from lib.maps import map_densepose_to_tex


def main(img_file, iuv_file):
    img = cv2.imread(img_file) / 255.
    iuv_img = cv2.imread(iuv_file)
    unwrap = (map_densepose_to_tex(img, iuv_img, 512) * 255).astype(np.int32)
    out_file = os.path.basename(img_file)
    cv2.imwrite(f"out/unwrap_{out_file}", unwrap)


if __name__ == '__main__':
    parser = argparse.ArgumentParser()
    parser.add_argument('image', type=str, help="Input image")
    parser.add_argument('iuv', type=str, help="Densepose IUV image")
    args = parser.parse_args()
    print(args)

    main(args.image, args.iuv)

実行

python unwrap.py spotlight_001.jpg spotlight_001.0001.png

出力

だいぶスカスカのtexture mapになるが、正面から見た一枚のみから抽出した部分的なものなのでこうなる。

ちなみに論文だと、これを入力としてpix2pixの形式でnormal mapとdisplacement mapを予測するよう学習し、入力画像の3d形状を推定している。

2023-10-29

pytorch3dのTextureUVでSMPLのmeshにtextureを貼る

3dの人体形状モデルとして有名なものにSMPLというのがあり、形状(shape)と姿勢(pose)を指定することで様々な人体形状のmeshを作り出せる。
https://smpl.is.tue.mpg.de/

SMPL自体はmeshを生成するものだが、対応するtexture mapも配布されていて、3d生成関連の論文読んでいるとよく使われているのを見かける。なので勉強がてらpytorch3dを使ってSMPLのmodelにtextureを貼ってみたのでメモ。

pytorch3dのinstall

手順はこちらに従う
https://github.com/facebookresearch/pytorch3d/blob/28f914b/INSTALL.md

mac環境なのでcudaは気にせずpipで入れた

pip install torch==1.13.0 torchvision
MACOSX_DEPLOYMENT_TARGET=10.14 CC=clang CXX=clang++  pip install "git+https://github.com/facebookresearch/pytorch3d.git@stable"

2.0系だとビルド時にエラーが出たので1.13.0を使っておいた。pytorch3dのinstall時点でpytorchが入ってないと依存でエラーになるので先にpytorchだけ入れておく。

ちなみにエラー内容としてはc+17が有効になってないというものだった。私の環境ではclang 14.0が入っていてc+17がデフォルトになってないversionだったためと思われる。
https://cpprefjp.github.io/implementation.html#clang

clang 16.0以降を使う、またはビルド時にc+17を使うようフラグを渡せばpytorch2系でもOKなはずだが目的から外れるのでとりあえずこのまま。

SMPLの準備

python環境かつuv座標の情報が必要なので SMPL for Python Users > Download UV map in OBJ format からダウンロードする。ちなみに取得にはメアドでのユーザ登録が必要。
https://smpl.is.tue.mpg.de/download.php

zipを開くとobjファイルと一緒にtexture mapのサンプルも入ってるのでこれを使うことにする。

pytorch3dによる描画

denseposeのtextureをSMPLに貼り付けるチュートリアルがあるのでこれと同じ形でOK
https://pytorch3d.org/tutorials/render_densepose

densepose -> smplへのuv map変換処理を除いて単純にTexture, Meshを作ればよいはず

with Image.open(tex_path) as image:
    np_image = np.asarray(image.convert("RGB")).astype(np.float32)
tex = torch.from_numpy(np_image / 255.)[None].to(device)

verts, faces, aux = load_obj(obj_path)
texture = renderer.TexturesUV(maps=tex, faces_uvs=[faces.verts_idx], verts_uvs=[aux.verts_uvs])
mesh = Meshes([verts], [faces.verts_idx], texture)

ということで描画してみるとこうなる網目が完全に崩れているので何かおかしい

TextureUVの定義はこれ
https://github.com/facebookresearch/pytorch3d/blob/297020a4b1d7492190cb4a909cafbd2c81a12cb5/pytorch3d/renderer/mesh/textures.py#L612

faces_uvs: 各faceを形作る頂点indexのtensor
verts_uvs: 頂点毎のuv座標を与えるtensor

と書いてあるので良さそうに思える。

実際に渡しているデータを調べてみるとvertsとverts_uvsのデータ数が合っていない

verts, faces, aux = load_obj(obj_path)
print(verts.shape)    # torch.Size([6890, 3])
print(aux.verts_uvs)  # torch.Size([7576, 2])

SMPLのmeshの頂点数は6890個なのでverts_uvsのデータ数がそれより多くなっている模様。facesのデータを見てみるとこう

verts, faces, aux = load_obj(obj_path)
print(faces.verts_idx.shape)          # torch.Size([13776, 3])
print(torch.max(faces.verts_idx))     # tensor(6889)
print(faces.textures_idx.shape)       # torch.Size([13776, 3]) 
print(torch.max(faces.textures_idx))  # tensor(7575)

faces.textures_idxがaux.verts_uvsのindexと対応しているということだった。

見る方向による色の違いを表現するため、mesh頂点毎にuv座標を指定するのではなく、同じ頂点でも別のfaceの場合は異なるuv座標が対応するとのこと
https://github.com/pmh47/dirt/issues/46#issuecomment-540392773

TextureUVの引数を修正して

texture = renderer.TexturesUV(maps=tex, faces_uvs=[faces.textures_idx], verts_uvs=[aux.verts_uvs])

とすることでちゃんと網目の模様になった

import os
import torch
import matplotlib.pyplot as plt
import numpy as np
from PIL import Image
from pytorch3d.structures import Meshes
import pytorch3d.renderer as renderer
from pytorch3d.io import load_obj


device = torch.device("cpu")
    

def create_renderer():
    R, T = renderer.look_at_view_transform(1.0, 0, 0) 
    cameras = renderer.FoVPerspectiveCameras(device=device, R=R, T=T)

    raster_settings = renderer.RasterizationSettings(
        image_size=512, 
        blur_radius=0.0, 
        faces_per_pixel=1, 
    )
    lights = renderer.PointLights(device=device, location=[[0.0, 0.0, 2.0]])

    return renderer.MeshRenderer(
        rasterizer=renderer.MeshRasterizer(
            cameras=cameras, 
            raster_settings=raster_settings
        ),
        shader=renderer.SoftPhongShader(
            device=device, 
            cameras=cameras,
            lights=lights
        )
    )


# downloadしたSMPLのzipを展開してこのpathに置いておく
DATA_DIR = "./data"
tex_path = os.path.join(DATA_DIR, "smpl/smpl_uv_20200910.png")
obj_path = os.path.join(DATA_DIR, "smpl/smpl_uv.obj")


with Image.open(tex_path) as image:
    np_image = np.asarray(image.convert("RGB")).astype(np.float32)
tex = torch.from_numpy(np_image / 255.)[None].to(device)

verts, faces, aux = load_obj(obj_path)
texture = renderer.TexturesUV(maps=tex, faces_uvs=[faces.verts_idx], verts_uvs=[aux.verts_uvs])
mesh = Meshes([verts], [faces.verts_idx], texture)

renderer = create_renderer()
images = renderer(mesh)
plt.figure(figsize=(10, 10))
plt.imshow(images[0, ..., :3].cpu().numpy())
plt.axis("off");
plt.show()