テキスト感情分類(マルチラベル)

pytorch machine learning

こちらの記事で追加でやってみると書いたことのいくつかについてやったのでメモ
https://jsapachehtml.hatenablog.com/entry/2021/01/17/142444

マルチラベル分類

参考にしたこちらの論文と同じ形にして精度を比べてみることにした（英語のデータセットで）
https://arxiv.org/abs/1812.01207

マルチラベル分類にするための修正はこちら

  • lossの計算にbinary cross entropyを使う
    • ラベル毎に0 or 1を出力したいため
  • 評価用の出力をラベル毎にTrue/Falseの混同行列に変更

元のコードからの差分はこんな感じ
https://github.com/y-kamiya/emotion-classification/commit/e2f25685f9eedbba40db4a9bcecc5821ede3442f
細かい部分の修正は別コミットでもしているが大枠として

コードの全体はこちら
https://github.com/y-kamiya/emotion-classification/blob/feature/multi-labels/trainer.py

マルチラベル時とそうでない場合をオプションで変更して処理分けする形で実装してしまったのでちょっとわかりにくい。特にlabelsの扱いがマルチラベルの場合だけonehot表現になっているので注意

datasetの処理は特に汎用化せずSemEval2018 E-c専用。データ自体はこんなフォーマットになっている

ID  Tweet   anger   anticipation    disgust fear    joy love    optimism    pessimism   sadness surprise    trust
2017-En-21441   “Worry is a down payment on a problem you may never have'.  Joyce Meyer.  #motivation #leadership #worry    0   1   0   0   0   0   1   0   0   0   1
2017-En-31535   Whatever you decide to do make sure it makes you #happy.    0   0   0   0   1   1   1   0   0   0   0
...
メトリック修正

混同行列を表示する部分をマルチラベルの形に修正

def __log_confusion_matrix(self, all_preds, all_labels, epoch):
        buf = io.BytesIO()
        label_map = {value: key for key, value in self.config.dataset_class.label_index_map.items()}

        np.set_printoptions(precision=3)

        if self.config.multi_labels:
            fig, axes = plt.subplots(1, len(label_map.keys()), figsize=(25, 5))
            cm = metrics.multilabel_confusion_matrix(y_pred=all_preds.numpy(), y_true=all_labels.numpy())
            for i in range(len(label_map.keys())):
                # 表示を慣れた形にするため軸を入れ替え
                mat = np.array([[cm[i][1][1], cm[i][1][0]], [cm[i][0][1], cm[i][0][0]]])
                result = mat / mat.sum(axis=1, keepdims=True)
                print(f'{label_map[i]}\n{result}\n')

                display = metrics.ConfusionMatrixDisplay(result, display_labels=['P', 'N'])
                display.plot(ax=axes[i], cmap=plt.cm.Blues, values_format='.2f')
                display.ax_.set_title(label_map[i])
                display.ax_.set_ylabel('True label' if i == 0 else '')
                display.ax_.set_yticklabels(['P', 'N'] if i == 0 else [])
                display.im_.colorbar.remove()

            plt.subplots_adjust(wspace=0.1, hspace=0.1)
            fig.colorbar(display.im_, ax=axes)
            plt.savefig(buf, format="png", dpi=180)

scikit learnにはマルチラベル用の混同行列を計算するメソッドが用意されている
https://scikit-learn.org/stable/modules/generated/sklearn.metrics.multilabel_confusion_matrix.html

各ラベルに対して2x2の混同行列を出力する形だが、True Positiveが右下となっておりよく見る形とは反転しているため、こちらで書かれているような形に修正して表示した
https://aidemy.net/courses/2010/exercises/Sy2YnLsLeG#:~:text=%E6%B7%B7%E5%90%8C%E8%A1%8C%E5%88%97%E3%81%A8%E3%81%AF%E3%80%81%E5%90%84,%E3%82%92%E3%81%BE%E3%81%A8%E3%82%81%E3%81%9F%E8%A1%A8%E3%81%A7%E3%81%99%E3%80%82

分類用headのカスタマイズ

論文に合わせて分類用のheadを変更した

class CustomClassificationHead(nn.Module):
    def __init__(self, config, input_dim):
        super().__init__()
        self.config = config

        self.fc1 = nn.Linear(input_dim, 4096)
        self.fc2 = nn.Linear(4096, 2048)
        self.fc3 = nn.Linear(2048, 1024)
        self.fc4 = nn.Linear(1024, config.n_labels)
        self.dropout = nn.Dropout(p=0.3)
        self.prelu1 = nn.PReLU()
        self.prelu2 = nn.PReLU()
        self.prelu3 = nn.PReLU()

        nn.init.kaiming_normal_(self.fc1.weight)
        nn.init.kaiming_normal_(self.fc2.weight)
        nn.init.kaiming_normal_(self.fc3.weight)
        nn.init.kaiming_normal_(self.fc4.weight)

    def forward(self, x):
        # dropout is applied before this method is called
        # https://github.com/huggingface/transformers/blob/v4.1.1/src/transformers/models/bert/modeling_bert.py#L1380
        x = self.prelu1(self.fc1(x))
        x = self.prelu2(self.fc2(self.dropout(x)))
        x = self.prelu3(self.fc3(self.dropout(x)))
        return self.fc4(self.dropout(x))

論文ではこのように書かれている

MLP(4096 → 2048 → 1024 → nc) with PReLU and 0.3 dropout

BertForSequenceClassificationはマルチクラス分類のときと同様に使い、classifierだけ上書きすることで簡単に変更できた
https://github.com/y-kamiya/emotion-classification/blob/232b09bf994148de987ab65346ddf699668187e1/trainer.py#L175

ちなみにBertForSequenceClassificationはこうなっている

class BertForSequenceClassification(BertPreTrainedModel):
    def __init__(self, config):
        super().__init__(config)
        self.num_labels = config.num_labels

        self.bert = BertModel(config)
        self.dropout = nn.Dropout(config.hidden_dropout_prob)
        self.classifier = nn.Linear(config.hidden_size, config.num_labels)

        self.init_weights()

    def forward(...):
        ...
        pooled_output = outputs[1]

        pooled_output = self.dropout(pooled_output)
        logits = self.classifier(pooled_output)
        ...

BertModelにdropoutを適用したものがclassifierの入力となっているため、CustomClassificationHead側では最初にdropoutを含めないようにした。重みの初期化も入れとく必要があるので注意。

また、学習率のwarmupも行っていたのでそれも入れた

self.warmup_scheduler = optim.lr_scheduler.LambdaLR(self.optimizer, lr_lambda=lambda step: min(1.0, (step + 1) / config.warmup_steps))

1×10−5 (constant after 1/2 epoch linear warmup)

実験

semeval2018 E-cデータセットをそのまま使って学習・評価を行った。前回と同じくgoogle colabを利用。

実行コマンド

!python trainer.py --dataroot "$DATAROOT/semeval2018" --lang 'en' --batch_size 96 --epochs 50  --log_interval 36 --eval_interval 2 --fp16 --lr 1e-5 --name lr1e-5_warmup_customhead --dataset_class_name SemEval2018EmotionDataset --no_save --warmup_steps 36 --custom_head
!python trainer.py --dataroot "$DATAROOT/semeval2018" --lang 'en' --batch_size 96 --epochs 50  --log_interval 36 --eval_interval 2 --fp16 --lr 1e-5 --name lr1e-5_customhead --dataset_class_name SemEval2018EmotionDataset --no_save --custom_head
!python trainer.py --dataroot "$DATAROOT/semeval2018" --lang 'en' --batch_size 96 --epochs 50  --log_interval 36 --eval_interval 2 --fp16 --lr 1e-5 --name lr1e-5 --dataset_class_name SemEval2018EmotionDataset --no_save

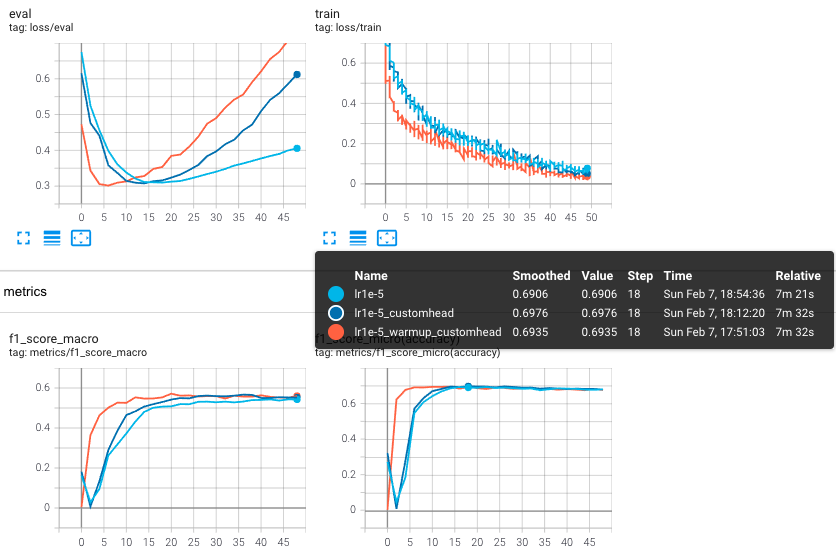
論文とは関係ない部分だが、どのくらい違いあるのか気になったので--custom_headの有無、--warmup_stepsの有無で試して比較してみた f:id:y-kamiya:20210211110332p:plain

最終的に精度が飽和する部分の値はどれも同程度。最大値となる部分を比べると元のheadを使う場合は若干低い値となっている。スコアの立ち上がりはwarmupを使う場合が明らかに早いため、学習に時間がかかるものの場合は特に重要そう。ただ、custom headを使った場合のスコアはwarmupの有無で多少異なり、warmupのあり/なしでそれぞれ0.6950, 0.6976だった(誤差の範囲かもしれないが)

論文との比較ということで5 epochだけ学習させた場合のスコアがこちら(custom headかつwarmupあり)

  • f1 micro: 0.673
  • f1 macro: 0.464
|           |        0 |       1 |        2 |       3 |        4 |       5 |        6 |       7 |       8 |       9 |      10 |   micro avg |   macro avg |   weighted avg |   samples avg |
|-----------|----------|---------|----------|---------|----------|---------|----------|---------|---------|---------|---------|-------------|-------------|----------------|---------------|
| precision |    0.785 |   0.000 |    0.722 |   0.849 |    0.854 |   0.699 |    0.698 |   0.453 |   0.781 |   0.000 |   0.000 |       0.760 |       0.531 |          0.683 |         0.723 |
| recall    |    0.779 |   0.000 |    0.781 |   0.497 |    0.794 |   0.453 |    0.791 |   0.192 |   0.592 |   0.000 |   0.000 |       0.620 |       0.444 |          0.620 |         0.639 |
| f1-score  |    0.782 |   0.000 |    0.750 |   0.627 |    0.823 |   0.550 |    0.742 |   0.270 |   0.673 |   0.000 |   0.000 |       0.683 |       0.474 |          0.642 |         0.648 |
| support   | 1101.000 | 425.000 | 1099.000 | 485.000 | 1442.000 | 516.000 | 1143.000 | 375.000 | 960.000 | 170.000 | 153.000 |    7869.000 |    7869.000 |       7869.000 |      7869.000 |

論文で書かれたスコアはこちら f:id:y-kamiya:20210211111109p:plain f:id:y-kamiya:20210211122502p:plain

microスコアは論文より若干低い程度だが、macroスコアが論文と比べて大きく下がっている。macroはラベル毎のスコアを出してから単純に平均を取るだけなので、ラベル毎のデータ数の差を考慮せずに等しく扱って平均を取っている。つまりデータ数が少ないことによってスコアが低いラベルがあればそれに引きづられて低いスコアになりやすい。

ラベル毎のスコアを見ると一目瞭然で、今回学習したものはデータ数が少ないラベル３種類で0%という結果になっている。これはさすがに何かおかしい気がするものの、データ数の多いラベルに引きづられてそちらを出力してしまったのかもしれない。

参考